Whole Number Theory

a whole number that cannot be divided exactly by 2; it has a remainder of 1.

For example, 1, 3, 5, 7, ...

a whole number that can be divided exactly by 2 (no remainder).

For example, 2, 4, 6, 8, ...

whole number greater than 1 that can only be divided exactly between itself and 1. (A prime number only has 2 factors.)

For example, 1, 2, 3, 5, 7, ...

the product when an integer is multiplied by itself.

For example, 2 × 2 = 4, 3 × 3 = 9 and so on.

the product when an integer is multiplied by itself twice.

For example, 2 × 2 × 2 = 8, 3 × 3 × 3 = 27 and so on.

the number that produces a number when it is multiplied by itself.

For example, √25 is 5 because 5 × 5 = 25.

he number that produces a number when it is multiplied by itself and then by itself again.

For example, ∛8 is 2 because 2 × 2 × 2 = 8.

number that divides exactly into another number without a remainder.

For example, factors of 6 are 1, 2, 3 and 6.

...of a number is found when you multiply that number by a whole number.

For example, multiples of 3 are 3, 6, 9, 12, ...

a multiple shared by 2 or more numbers.

For example, multiples of 2 are 2, 4, 6, 8, 10, 12, ... Multiples of 3 are 3, 6, 9, 12, ... 6 and 12 are common multiples of 2 and 3.

 a factor shared by 2 or more numbers. 1 is a common factor of all numbers.

For example, factors of 6 are 1, 2, 3 and 6. Factors of 12 are 1, 2, 3, 4, 6 and 12. Common factors of 6 and 12 are 1, 2, 3 and 6. 

To find all the factors of a large number, you can use a factor tree to list all its prime factors.

A factor tree is created by continually splitting a number into factors until only its prime factors remain.

Below are two examples of factor trees for 90.

         OR         

Both trees show that:

90 = 2 × 3 × 3 × 5   = 2 × 3² × 5

Use prime factors

You can find factors of large numbers using their prime factors.

EXAMPLE

Use the prime factors of 420 to find at least four other factors.

420 = 2 × 2 × 3 × 5 × 7

Other factors are:
2 × 2 = 4
2 × 3 = 6
2 × 5 = 10
5 × 7 = 35
2 × 3 × 5 = 30
2 × 2 × 3 × 7 = 84

To find the lowest common multiple, systematically test the multiples of the largest number until you find the first one that all the other numbers go into.

Steps to find the HCF

1. List all the factors for each number.

2. Select the largest number that is common to all lists.

EXAMPLE 1

Find the HCF of 16 and 24.

SOLUTION

First, write down all the factors of both numbers.

NumberFactors 

161, 2, 4, 8, 16

241, 2, 3, 4, 6, 8, 12, 24

The common factors are shown in red.

Find lowest common multiple

The LCM of two large numbers is the larger number multiplied by any additional prime factors in the smaller number that are not common to both

EXAMPLE

Find the LCM of 24 and 300.

SOLUTION

Match the prime factor from the trees:

The only additional prime factor for 24 is 2.

LCM = 300 × 2   = 600

Find highest common factor

The HCF of two large numbers is the product of the prime factors that are common to both the numbers.

Factor trees and prime factors can be used to find the highest common factors (HCF) or lowest common multiple (LCM) of sets of numbers.

Find highest common factor

The HCF of two large numbers is the product of the prime factors that are common to both the numbers.

EXAMPLE

Find the HCF of 144 and 324 by using prime factors.

SOLUTION

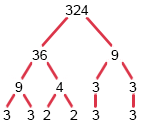
From the factor trees:

144 = 2 × 2 × 2 × 2 × 3 × 3

324 = 2 × 2 × 3 × 3 × 3 × 3

The prime factors that are common to both numbers are in red. These factors are: 2, 2, 3, 3.

HCF = 2 × 2 × 3 × 3   = 36