Maths Revision Cards
- Created by: Mx.Leah
- Created on: 05-01-20 16:32
Unit1
UNIT ONE REVISION
- Tasks
- Significant Figures
- Prime Factors
- Standard Form
- Surds
- Rationalising Fractions
- Powers
Tasks
When there are m ways to do one task and n ways to do another task. The total number of ways to do both tasks is m x n.
Significant Figures
You can round numbers to 1 or 2 significant figures to estimate the answer to calculations. Includes roots and surds.
Prime Factors
You can use a prime factor tree to write a number as the product of its prime factors.
You can use a venn diagram of prime factors to work out the HCF and LCM of two numbers.
The prime factor decomposition is when a number is written out as a product of its prime factors. It's usually written in index form.
Powers
When multiplying powers, add the indices
When dividing powers, subtract the indices
To raise a power to another power, multiply the indices.
Standard Form
A number in standard form is written in the form:
To write a number in standard form:
- Work out the value of
- Work out how many times must be multiplied or divided by 10 to find the value of
Surds
To simplify a surd, identify any factors that are square numbers.
Rationalising Fractions
To rationalise a fraction, multiply the numerator and the denominator by the surd in the denominator and simplify.
Unit2
UNIT TWO REVISION
- Identities
- Equations
- Expressions
- Sequences
- Double Brackets
- Quadratic Expressions
- Formulae
Identities
When two sides of a relation are equal for all values of it is called an identity.
An Identity has an equals sign and is true for all values of
Equations
An equation is only true for certain values of
To solve an equation involving fractions, multiply each term on each side by the LCM of the denominators.
An equation has an equals sign, terms in one letter and numbers that you can solve to find the value of the letter.
Expressions
Contains letters and number terms but doesn't have an equals sign.
You can simplify expressions if necessary.
Quadratic Expressions
A quadratic expression has a squared term (and no higher power)
Formulae
A formula has an equals sign and letters to represent different quantities.
The letters are variables as the quantities can vary.
Sequences
In an arithmetic sequence, the terms increase or decrease by a fixed number called the common difference.
In a fibonacci - like sequence, the next number is found by adding the previous two numbers together.
In a geometric sequence, the terms increase or decrease by a constant multiplier.
A quadractic sequence has and no higher power of in its nth term.
Brackets
To expand double brackets, multiply each term in one bracket by each term in the other bracket.
To square a single bracket, multiply the bracket by itself, then expand and simplify.
Unit3
UNIT THREE REVISION
- Stem and Leaf diagrams
- Frequency Polygons
- Modal class intervals
- Scatter Graphs
- Line of best fit
- Time Series
Stem and Leaf Diagrams
A back to back stem and leaf diagram compares two sets of results. On the left hand side the numbers are read as backwards.
Frequency polygons
A Frequency polygon is a graph made by joining the midpoints of the tops of a bar chart with straight lines.
A quicker way to draw frequency polygons is to plot the frequency against midpoints of each group.
Modal Class Intervals
The modal class (or modal group) has the highest frequency.
To estimate a mean from a grouped frequency table, add together the products of class midpoints and their frequencies and divide by the total frequency.
If the total frequency in a grouped freqency table is , then the median lies in the group containing the th item of data.
Scatter Graphs
Bivariate data is data that has two variables. Points can be placed in a scatter graph to see if there is a correlation between them.
Positive correlation - When points lie close to an upwards facing line
Negative correlation - When points lie close to a downwards facing line.
No correlation - Points create no discernable line.
Line Of Best Fit
A line of best fit is the line that passes as close as possible to the points on a scatter graph.
Using a line of best fit to predict data values within the range of data is called interpolation and is usually reasonably accurate.
Using a line of best fit to predict data values outside the range of data is called extrapolation and may not be accurate.
Individual points which are outside the overall pattern of a scatter graph are called outliers. They can be removed from a data set provided a reason for their removal is given.
Time Series
A time series graph is a time graph with time plotted on the horizontal axis.
Unit4
UNIT FOUR REVISION
- Mixed Numbers
- Reciprocals
- Unit Ratios
- Direct Proportion
- Interest
- VAT
- Recurring Decimals
Mixed Numbers
It is often easier to write mixed numbers as improper fractions before doing a calculation
1 3/4 + 2 3/8
7/4 + 19/8 = 418
Reciprocals
The reciprocal of the number is .
To find the reciprocal of a fraction, swap the numerator with the denominator.
To find the reciprocal of a mixed number, first convert it into an improper fraction.
Unit Ratios
You can compare ratios by writing them as unit ratios. In a unit ratio, one of the numbers is 1. The other number may or may not be a whole number.
To share a quantity in a given ratio you could work out what fraction of the total amount each person recieves and then multiply that fraction by the total amount.
Proportion
When two quantities are in direct proportion, as one is multiplied by a number , so is the other. Their ratio also stays the same as they increase or decrease.
Interest
Simple Interest is the interest calculated only on the original amount invested. It is the same each year.
You can calculate a percentage change using the formula:
You can use inverse operations to calculate the original amount after a percentage increase or decrease.
VAT
VAT - Value Added Tax
VAT is charged at 20% on most goods and services.
Domestic fuel bills have a lower VAT rate of 5%
On some things, VAT is not charged
Recurring Decimals
All recurring decimals can be written as exact fractions.
If 1 decimal place recurrs, multiply by 10.
If 2 decimal places recurr, multiply by 100.
If 3 decimal places recurr, multiply by 1000.
Unit5
UNIT FIVE REVISION
- Interior Angles
- Exterior Angles
- Angles on Straight Lines
- Angles in Polygons
- Pythagorus' Thereom
- SOHCAHTOA
- Adjacent, Opposite and Hypoteneuse
Interior Angles
The interior angles of a polygon are those angles at each vertex that are on the inside of the polygon. There is one per vertex.
For a regular polygon, by definition, all the interior angles are the same.
Exterior Angles
The Exterior Angle is the angle between any side of a shape, and a line extended from the next side. ... When we add up the Interior Angle and Exterior Angle we get a straight line 180°. They are "Supplementary Angles".
Angles on a Straight Line
The angles on a straight line add up to 180 degrees.
Pythagorus' Thereom
Pythagorus' Thereom states that in a right angled triangle, the square of the hypoteneuse is equal to the sum of the squares of the opposite and adjacent sides.
SOHCAHTOA
Sine = Opposite / Hypotenuse
Cosine = Adjacent / Hypotenuse
Tangent = Opposite / Adjacent
Adjacent, Opposite and Hypoteneuse
- "Opposite" is opposite to the angle θ
- "Adjacent" is adjacent (next to) to the angle θ
- "Hypotenuse" is the long one
Unit6
UNIT SIX REVISION
- Linear Equations
- Distance -Time Graphs
- Velocity - Time Graphs
- Reciprocal Functions
- Cubic Functions
Linear Equations
A linear equation is any equation involving one or two variables whose exponents are one. ex. = 4 is not a linear equation.
The equation for a straight-line graph can be written as:
A linear function has a graph that is a straight line.
Distance -Time Graphs
If an object moves along a straight line, the distance travelled can be represented by a distance-time graph. In a distance-time graph, the gradient of the line is equal to the speed of the object. The greater the gradient (and the steeper the line) the faster the object is moving.
Velocity - Time Graphs
If an object moves along a straight line, the distance travelled can be represented by a distance-time graph. In a distance-time graph, the gradient of the line is equal to the speed of the object. The greater the gradient (and the steeper the line) the faster the object is moving.
Reciprocal Functions
The graphs of reciprocal functions are made up of branches, which are the two main parts of the graph; and asymptotes, which are horizontal and vertical lines that the graph approaches but doesn't touch.
Cubic Functions
In mathematics, a cubic function is a function of the form where the coefficients a, b, c, and d are real numbers, and the variable x takes real values, and a ≠ 0. In other words, it is both a polynomial function of degree three, and a real function.
Unit7
UNIT SEVEN REVISION
- Area of Shapes
- Error Intervals
- Volumes
- Capacity
- Surface Areas
- Area of Circle
Area of Shapes
- Area of Trapezium = 1/2( a + b )h
- Area of a Rectangle = Base × Height
- Area of a Square = Base × Height
- Area of Triangle = ½(Base × Height)
- Area of Parallelogram = Base × Height
- Area of Trapezoid = ½(Base1 + Base2) × Height
- Area of Circle = π(radius)2 = πr2
Error Intervals
An error interval is the range of values that a number could have taken before being rounded or truncated. Error intervals are usually written as a range using inequalities, with a lower bound and an upper bound.
Volumes
:max_bytes(150000):strip_icc()/surface-area-and-volume-2312247-v5-5b57857e46e0fb00251665b9.png)
Capacity
The amount that something can hold. Usually it means volume, such as milliliters (ml) or liters (l) in Metric, or pints or gallons in Imperial.
Surface Areas

Area of a Circle
In geometry, the area enclosed by a circle of radius r is π r². Here the Greek letter π represents a constant, approximately equal to 3.14159, which is equal to the ratio of the circumference of any circle to its diameter.
Unit8
UNIT EIGHT REVISION
- Plans and Elevations
- Transformations
- Bearings
- Bisectors
Plans and Elevations

Transformations
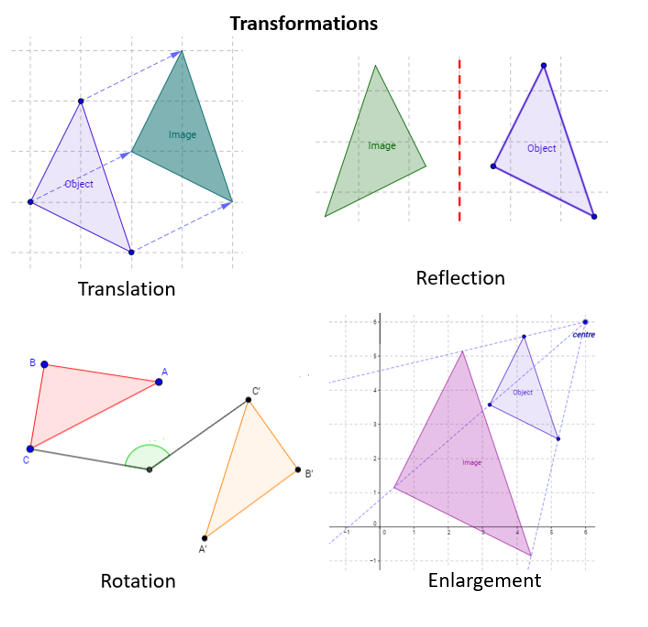
Transformations
There are four main types of transformations: translation, rotation, reflection and dilation. These transformations fall into two categories: rigid transformations that do not change the shape or size of the preimage and non-rigid transformations that change the size but not the shape of the preimage.
Bearings
A bearing measures the movement of an angle in a clockwise direction and always on the north line. The bearing of a point is the line joining the centre of the compass through the point measured in degrees in a clockwise way from the north direction.
Bisectors
A bisector is something that cuts an object into two equal parts. It is applied to angles and line segments. In verb form, we say that it bisects the other object.
Unit9
UNIT NINE REVISION
- Solving Quadratics
- Perfect Squares
- Completing The Square
- Simultaneous Equations
- Inequalities
- Set Notation
Solving Quadratics
To solve a quadratic equation by factoring,
- Put all terms on one side of the equal sign, leaving zero on the other side.
- Factor.
- Set each factor equal to zero.
- Solve each of these equations.
- Check by inserting your answer in the original equation.
Perfect Squares
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it can be written as 3 × 3. ... Square numbers are non-negative.
Completing the Square
Completing the Square is a method used to solve a quadratic equation by changing the form of the equation so that the left side is a perfect square trinomial .
Simultaneous Equations
In mathematics, a set of simultaneous equations is a finite set of equations for which common solutions are sought.
- Step 1: Multiply each equation by a suitable number so that the two equations have the same leading coefficient. ...
- Step 2: Subtract the second equation from the first.
- Step 3: Solve this new equation for y.
- Step 4: Substitute y = 2 into either Equation 1 or Equation 2 above and solve for x.
Inequalities
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size.
Set Notations
Set notation is used to help define the elements of a set. The symbols shown in this lesson are very appropriate in the realm of mathematics and in mathematical logic. When done properly, a set described in words or in symbols will clearly show all the elements of that set.
Unit10
UNIT TEN REVISION
- Sample Space Diagrams
- Tree Diagrams
- Conditional Probability
Sample space diagrams
In probability theory, the sample space of an experiment or random trial is the set of all possible outcomes or results of that experiment. A sample space is usually denoted using set notation, and the possible ordered outcomes are listed as elements in the set.
Tree Diagrams
In probability theory, a tree diagram may be used to represent a probability space. Tree diagrams may represent a series of independent events or conditional probabilities. Each node on the diagram represents an event and is associated with the probability of that event.

Conditional Probability
Conditional probability is the probability of one event occurring with some relationship to one or more other events. For example: Event A is that it is raining outside, and it has a 0.3 (30%) chance of raining today. Event B is that you will need to go outside, and that has a probability of 0.5 (50%).
Unit11
UNIT ELEVEN REVISION
- Compound Interest
- Compound Measures
- Density
Compound Interest
Compound interest is the addition of interest to the principal sum of a loan or deposit, or in other words, interest on interest. It is the result of reinvesting interest, rather than paying it out, so that interest in the next period is then earned on the principal sum plus previously accumulated interest.
Compound Measures
Compound Measures
A Compound measurement is a measurement that uses more than one quantity.
Examples include density measurements, speed measurements and rates of pay.
Density
Density is calculated by mass ÷ volume. So density is therefore written as mass per volume.
The most common units used to measure density are kg/m3
The density of pure water is always 1000kgm-3. So anything with a lower density will float in water.
Speed
Speed is measured using the formula distance ÷ time. So this will therefore be written as distance per time.
Density
Density is a measure of mass per volume. The average density of an object equals its total mass divided by its total volume. An object made from a comparatively dense material (such as iron) will have less volume than an object of equal mass made from some less dense substance (such as water).
Unit12
UNIT TWELVE REVISION
- Congruency
- Enlargement
Congruency
In geometry, two figures or objects are congruent if they have the same shape and size, or if one has the same shape and size as the mirror image of the other.
Two Triangles are congruent when one of these conditions of congruency are true.
SAS
SSS
ASA
AAS
RHS
Enlargement
Transformations change the size or position of shapes. Congruent shapes are identical, but may be reflected, rotated or translated. Scale factors can increase or decrease the size of a shape.
Unit13
UNIT THIRTEEN REVISION
- Sine Graph
- Cosine Graph
- Tangent Graph
- Sine Rule
- Cosine Rule
Sine Graph
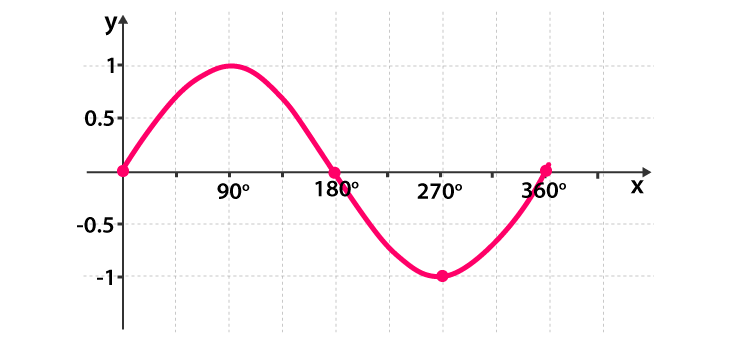
Cosine Graph
Tangent Graph
Sine Rule
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of a triangle to the sines of its angles.
Cosine Rule
In trigonometry, the law of cosines relates the lengths of the sides of a triangle to the cosine of one of its angles.
The law of cosines states where γ denotes the angle contained between sides of lengths a and b and opposite the side of length c.
Unit14
UNIT FOURTEEN REVISION
- Sample Sizes
- Stratified Samples
- Cumulative Frequency
- Box Plot
- Histograms
Sample Sizes
Sample size measures the number of individual samples measured or observations used in a survey or experiment. For example, if you test 100 samples of soil for evidence of acid rain, your sample size is 100. If an online survey returned 30,500 completed questionnaires, your sample size is 30,500.
Stratified Samples
Stratified sampling refers to a type of sampling method . With stratified sampling, the researcher divides the population into separate groups, called strata. Then, a probability sample (often a simple random sample ) is drawn from each group.
Cumulative Frequency
Cumulative frequency analysis is the analysis of the frequency of occurrence of values of a phenomenon less than a reference value. The phenomenon may be time- or space-dependent. Cumulative frequency is also called frequency of non-exceedance.
Box Plots
In descriptive statistics, a box plot or boxplot is a method for graphically depicting groups of numerical data through their quartiles.
Histograms
A histogram is an accurate representation of the distribution of numerical data. It is an estimate of the probability distribution of a continuous variable.
It differs from a bar graph, in the sense that a bar graph relates two variables, but a histogram relates only one.
Unit16
UNIT SIXTEEN REVISION
- Circle Thereoms
- Circle Anatomy
Circle Anatomy
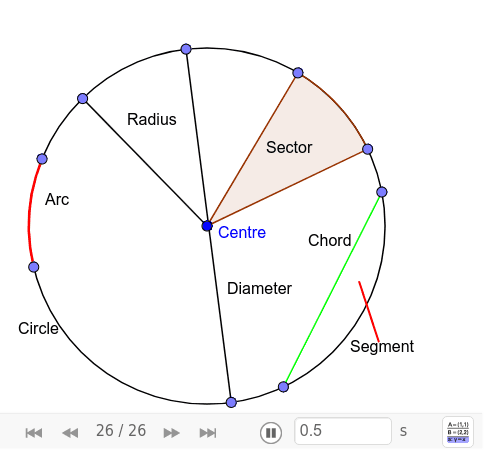
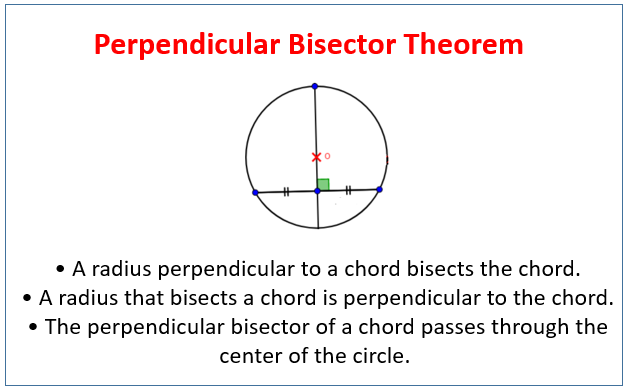
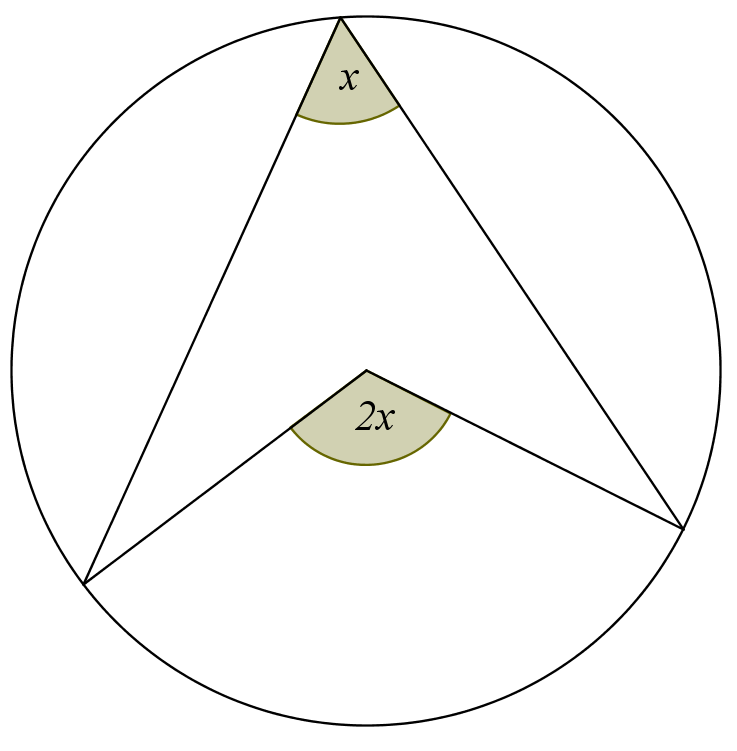
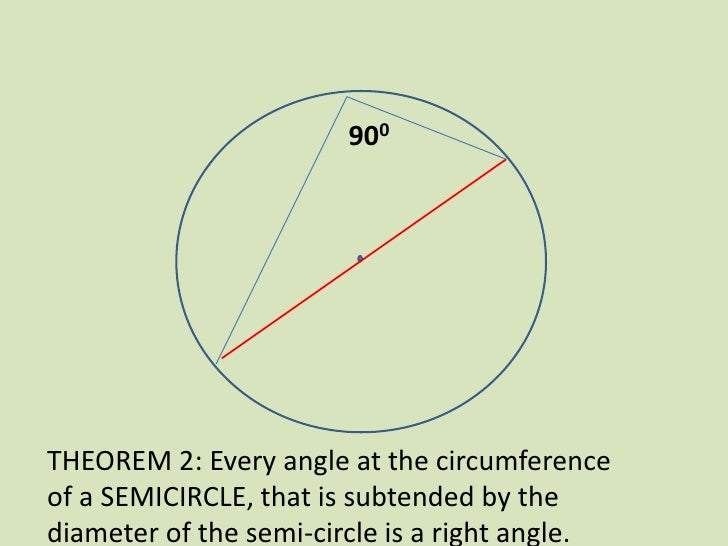
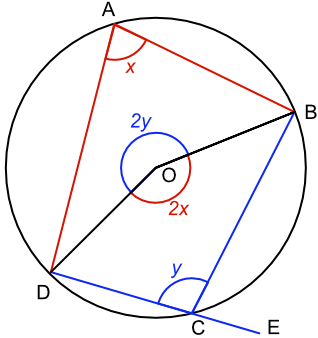
Circle Thereom
The angle between a tangent and the radius is equal to 90 degrees
Circle Thereom
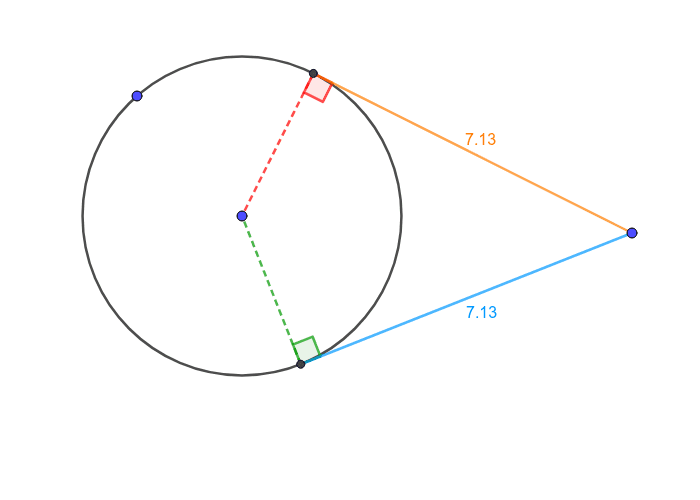
Circle Thereom
Circle Thereom
Circle Thereom

Circle Thereom
Circle Thereom
Circle Thereom
The alternate segment theorem (also known as the tangent-chord theorem) states that in any circle, the angle between a chord and a tangent through one of the end points of the chord is equal to the angle in the alternate segment.
Unit17
UNIT SEVENTEEN REVISION
- Subject of a formula
- Functions
- Inverse Functions
- Algebraic Proof
Subject of a Formula
- Make x the subject of the formula:
- 4y + 2 = x - 4.
- x = 4y + 6.
- Make y the subject of the formula.
- 2y/5 - 3x = 2.
- TIP: Remember to put brackets around 2 + 3x because both the 2 and the 3x are being multiplied by 5.
- y = 5 + 15x/2.
- - All it means is get a letter on one side of the equation on its own.
Functions
In mathematics, a function is a relation between sets that associates to every element of a first set exactly one element of the second set. Typical examples are functions from integers to integers or from the real numbers to real numbers.
It is commonly written as either f(x) or g(x) or both.
Inverse Functions
In mathematics, an inverse function (or anti-function) is a function that "reverses" another function: if the function f applied to an input x gives a result of y, then applying its inverse function g to y gives the result x, and vice versa, i.e., f(x) = y if and only if g(y) = x.
Algebraic Proof
An algebraic proof shows the logical arguments behind an algebraic solution. You are given a problem to solve, and sometimes its solution. If you are given the problem and its solution, then your job is to prove that the solution is right.
Use n to represent any integer.
2n=even
n-1 or 2n-1=odd
Unit18
UNIT EIGHTEEN REVISION
- Vectors
- Magnitude
- Displacement
Vectors
A vector is an object that has both a magnitude and a direction. Geometrically, we can picture a vector as a directed line segment, whose length is the magnitude of the vector and with an arrow indicating the direction. The direction of the vector is from its tail to its head.
Magnitude
The magnitude of a vector →PQ is the distance between the initial point P and the end point Q . In symbols the magnitude of →PQ is written as | →PQ | . If the coordinates of the initial point and the end point of a vector is given, the Distance Formula can be used to find its magnitude.
Displacement
A displacement is a vector whose length is the shortest distance from the initial to the final position of a point P. It quantifies both the distance and direction of an imaginary motion along a straight line from the initial position to the final position of the point.
Unit19
UNIT NINETEEN REVISION
- Direct Proportion
- Inverse Proportion
- Exponential Functions
Direct Proportion
With direct proportion, the two variables change at the same rate. Direct Proportion. With direct proportion, the two variable change at the same time. In direct proportion, as the first variable increases (decreases), the second variable also increases (decreases).
Indirect Proportion
An inverse variation occurs if one of the variables increases or decreases and the other variable decreases or increases. It can be read as “varies inversely” and “inverse proportion”. Inverse variation exists if the relationship exists between the two variables whose product is constant (k).
Exponential Functions
In mathematics, an exponential function is a function of the form. where b is a positive real number, and in which the argument x occurs as an exponent. For real numbers c and d, a function of the form is also an exponential function, as it can be rewritten as.
Related discussions on The Student Room
- len's y12 gyg blog »
- Tips for organising for A-levels »
- My year 10 gyg :) »
- is this good way of revising for gsces? »
- catching up on math-bio-chem a level w/out burnout »
- reuben's y13/medapps journey!! »
- Has/Will a deck of cards problem come up in the ENGAA/PAT? »
- Flash cards »
- Academic comeback gyg 2024 🎀 »
- Successful year 13 plan »

Comments
No comments have yet been made