Maths
Revision for end of year exams 2012.
- Created by: Former Member
- Created on: 25-05-12 19:04
Subtracting Negative Numbers
Subtracting Negative Numbers
If you subtract a positive number you move to the left of the number-line.
_________________________________________________
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
Example:
9-7=2 (start at 9 and move 7 to the left)
3-7=-4 (start at 3 and move 7 to the left)
-1-7=-8 (start at -1 and move 7 to the left)
Subtracting a Positive Number - Move to the left of the number-line
Subtracting a Negative Number - Move to the right of the number line
ALWAYS START FROM THE POSITION OF THE FIRST NUMBER!
Adding Negative Numbers
Adding Negative Numbers
If you add a positive number you move to the right of the number-line.
_________________________________________________
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 8 9 10
Example:
3+5=8 (start at 3 and move 5 to the right)
-4+5=1 (start at -4 and move 5 to the right)
-9+5=-4 (start at -9 and move 5 to the right)
Adding a Positive Number - Move to the right of the number-line
Adding a Negative Number - Move to the left of the number line
ALWAYS START FROM THE POSITION OF THE FIRST NUMBER!
Powers/Index/Exponent
Powers,Index and Exponents
A Power can somtimes be called an Index or Exponent. It tells the user how many lots of a particular number need to be multiplied together.
For Example:
The 3 is the power...
43
...And the 4 is the base number.
This means "4 to the power of 3" and tells you that 3 lots of 4 are to be multiplied together.
So, 43 = 4x4x4 = 64.
Factors
Factors
A whole number that can be divided cleanly into another whole number is called a factor of that number.
For Example:
1,2,3,4,6,9,12,18 and 36 are all factors of 36.
Factor Trees
36 = 2 x 2 x 3 x 3
/ \
9 4
/ \ / \
3 3 2 2
Lowest Common Multiple (LCM)
LCM
The smalest number that 2 numbers go into.
Example:
What are some common multiples of 2 and 3?
Multiples of 2: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24...
Multiples of 3: 3, 6, 9, 12, 15, 18, 21, 24, 27...
Common multiples of 2 and 3 include 6, 12, 18, and 24.
The lowest common multiple or least common multiple is the lowest multiple two numbers have in common.
The way to find the lowest common multiple is to do what we did above: write out a list of the lowest multiples of each number, and look for the lowest multiple both numbers have in common.
The LCM of 2 & 3 is 6.
Highest Common Factor (HCF)
HCF
The largest common factor of two or more numbers is called the highest common factor (HCF).
For Example:
The factors of 8 are 1, 8, 2 & 4
The factors of 12 are 1, 12, 2, 6, 3 & 4
So the common factors of 8 and 12 are 1,2 and 4 as they both go into them.
4 is the largest common factor of 8 and 12.
HCF = 4
Equivalent Fractions
Equivalent Fractions have the same value, even though they may look different.
These fractions are really the same:
1 - 2 = 2 - 4 = 4 - 8
Why are they the same? Because when you multiply or divide both the top and bottom by the same number, the fraction keeps it's value.
The rule to remember is:
What you do to the top of the fraction
you must also do to the bottom of the fraction !
Percentage Equivalents
Fractions can be turned into percentages.
For Example:
7 35
- = - = 35%
20 100
Percent means "over 100" so to turn a fraction into a percentage you need to turn the denominator into 100. In the example above, to turn 20 into 100 we had to times it by 5. After this we had to times the numerator by 5 as well. The numerator is the percentage.
Adding and Subtracting Fractions
To add or subtract fractions that have a common denominator, just add or subtract the numerators and put the result over the common denominator, like this:
But what if the fractions don’t have a common denominator? The answer is that they must then be converted to equivalent fractions that do have a common denominator.
You do this by finding the lowest number that both of the denominators go into and make that the new denominator. Multiply the numerator the number of times you multiplied the nominator of the same fraction. Finally add or subtract the two fractions.
Multiplying Fractions
There are 3 simple steps to multiply fractions
1. Multiply the top numbers (the numerators)
2. Multiply the bottom numbers (the denominators).
3. Simplify the fraction if needed.
Example:
Dividing Fractions
There are 3 Simple Steps to Divide Fractions:
- Turn the second fraction (the one you want to divide by) upside-down.
- Multiply the first fraction by the new second.
- Simplify the fraction (if needed)
For Example:
Rounding
How to Round Numbers
- Decide which is the last digit to keep
- Leave it the same if the next digit is less than 5 (this is called rounding down)
- But increase it by 1 if the next digit is 5 or more (this is called rounding up)
Example: Round 74 to the nearest 10
- We want to keep the "7" as it is in the 10s position
- The next digit is "4" which is less than 5, so no change is needed to "7"
Answer: 70
(74 gets "rounded down")
Long Multiplication
Long Division is a way to multiply numbers larger than 10.
Here is an example of long division:
612 × 24
- First we multiply 612 × 4 (=2,448),
- then we multiply 612 × 20 (=12,240),
- and last we add them together (2,448+12,240=14,688).
When we multiply 612 × 20 we only need to multiply 612 × 2 and place the result one column over (so it is the same as multiplying by 20).
We just have to be careful about lining up the columns.
Proportion
A proportion is an equation with a ratio on each side. It is a statement that two ratios are equal.
3/4 = 6/8 is an example of a proportion.
When one of the four numbers in a proportion is unknown, cross products may be used to find the unknown number. This is called solving the proportion. Question marks or letters are frequently used in place of the unknown number.
Example:
Solve for n: 1/2 = n/4.
Using cross products we see that the denominator of the first fraction is 2 and the second 4. To get from 2 to 4 we double the number (x2). Whatever you do to the denominator we do to the numerator so we have to multiply 1 by 2 which equals 2. n there for equals 2.
Ratio
A ratio is a pair of numbers that make a comparison. Specifically, a ratio compares two numbers using a fraction. They can be written in lots ways, for instance:
1 to 3
1:3
1/3
The best way to understand a ratio is to think of an example to explain it, and lets go for the old classic, coloured socks! Imagine I have a drawer that is full of red, yellow and blue socks. If I know the ratio of red, yellow and blue socks is described by 2:3:5 then I know that for every two red socks there will be three yellow and five blue. So the ratio tells us how to relate things to each other, and specifically what proportion they are in.
How to work out a ratio
Now let's take another classic example - school kids! If there are 18 girls and 12 boys in the class, then you might get asked to turn that into a ratio. All you do is put the numbers next to each other like this: 18:12 - and that's the ratio of girls to boys! Then you would normally reduce it to as low as you can - 3:2.
BODMAS
"Operations" mean things like add, subtract, multiply, divide, squaring, etc. If it isn't a number it is probably an operation.
But, when you see something like...
7 + (6 × 52 + 3)
... what part should you calculate first?
Calculate them in the wrong order, and you will get a wrong answer ! There are some rules when doing calculations, and they are:
B Brackets first O Orders (ie Powers and Square Roots, etc.) DM Division and Multiplication (left-to-right) AS Addition and Subtraction (left-to-right)
Alternate Interior Angles
Alternate Interior Angles
When two lines are crossed by another line (called the Transversal):
The pairs of angles on opposite sides of the transversal but inside the two lines are called Alternate Interior Angles.
In this example, these are Alternate Interior Angles:
- c and f are Alternate Interior Angles
- d and e are also Alternate Interior Angles
Alternate Exterior Angles
Alternate Exterior Angles
When two lines are crossed by another line (called the Transversal):
The pairs of angles on opposite sides of the transversal but outside the two lines are called Alternate Exterior Angles.
In the example:
- a and h are Alternate Exterior Angles
- b and g are also Alternate Exterior Angles (To help you remember: the angle pairs are on "Alternate" sides of the Transversal, and they are on the "Exterior" of the two crossed lines)
Corresponding Angles
When two lines are crossed by another line (called the Transversal):
The angles in matching corners are called Corresponding Angles.
In this example, these are corresponding angles:
- a and e
- b and f
- c and g
- d and h
Interior Angles of Polygons
An Interior Angle is an angle inside a shape.
The General Rule
Each time we add a side (triangle to quadrilateral, quadrilateral to pentagon, etc), we add another 180° to the total:
Shape Sides Sum of Interior Angles Shape Each Angle
Any Polygon n (n-2) x 180° (n-2) x 180° / n
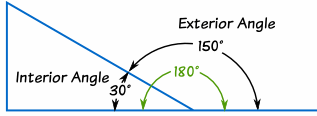
Exterior Angles of Polygons
The Exterior Angle is the angle between any side of a shape,
and a line extended from the next side.
The Exterior Angles of a Polygon add up to 360°
In other words the exterior angles add up to one full rotation. If the lines change direction and eventually return back to the start.
Note: This rule only works for simple polygons
Quadrilaterals
Quadrilateral means "four sides" (quad means four, lateral means side). Any four-sided shape is a Quadrilateral but the sides have to be straight, and it has to be 2-dimensional.
Properties
- Four sides (or edges)
- Four vertices (or corners).
- The interior angles add up to 360 degrees:
Constructions
"Construction" in Geometry means to draw shapes, angles or lines accurately.These constructions only use a pair of compasses, a ruler and a pencil.
Angle Bisector: Using a pair of compasses and a ruler to cut an angle in half
Equilateral Triangle: Drawing an equilateral triangle using a pair of compasses and a ruler.
Area of Simple Shapes
It is the amount of space inside the boundary of a flat object
Example:
These shapes all have the same area of 9:
What is the area of this rectangle?
The formula is:
Area = w × h
w = width
h = height
The width is 5, and the height is 3, so we know w = 5 and h = 3. So:
Area = 5 × 3 = 15
Area of Difficult Shapes
You can sometimes break a shape up into two or more simpler shapes:
Example: What is the area of this Shape?
Let's break the area into two parts:
Part A is a square:
Area of A = a2 = 20m × 20m = 400m2
Part B is a triangle. Viewed sideways it has a base of 20m and a height of 14m.
Area of B = ½b × h = ½ × 20m × 14m = 140m2
So the total area is:
Area = Area of A + Area of B = 400m2 + 140m2 = 540m2
Volume of Cuboids and Prisms
The volume of a cuboid is found using the formula:
Volume = Height × Width × Length
Which is usually shortened to:
V = h × w × l
Or:
V = hwl
(To remember, think "howl")
Surface Area of a Prism
The surface area is found using the formula:
A = 2wl + 2lh + 2hw
Example:
Find the volume and surface area of this cuboid.
V = 4×5×10 = 200
A = 2×4×5 + 2×5×10 + 2×10×4
= 40+100+80 = 220
Transformations
The three main Transformations are:
- Rotation (Turn)
- Reflection (Flip)
- Translaton (Slide)
After any of those transformations (turn, flip or slide), the shape still has the same size, area, angles and line lengths. If one shape can become another using Turns, Flips and/or Slides, then the two shapes are called Congruent.
The other important Transformation is enlargement. The shape becomes bigger or smaller. If you have to Enlarge to make one shape become another then the shapes are not Congruent, but they are Similar.
- If you only rotate, reflect or translate then shapes are congruent.
- If you need to enlarge then shapes are similar.
Circumference of a Circle
We can say:
Circumference = π × Diameter
Example: You walk around a circle which has a diameter of 100m, how far have you walked?
Distance walked = Circumference = π × 100m
= 314m (to the nearest m)
Brackets
Types of brackets include:
- parentheses or "round brackets" ( )
- "square brackets" or "box brackets" [ ]
- braces or "curly brackets" { }
- "angle brackets" < >
(Note: Angle brackets can be confusing because they look like the "less than" and "greater than" signs)
When you see things inside brackets you do them first:
Example: (3 + 2) × (6 - 4)
The parentheses group 3 and 2 together, and 6 and 4 together, so they get done first:
(3 + 2) × (6 - 4) = (5) × (2) = 5×2 = 10
Without the parentheses the multiplication would be done first:
3 + 2 × 6 - 4 = 3 + 12 - 4 = 11 (not 10)
Percentage Increase and Decrease
Percentage Incread or Decrease.
Example:
Increase £24 by 15%
10% of £24 is £2.40
5% of £24 is £1.20
________________
15% £3.60
- - - - - - - - - - - - - - - - - - - - - -
Increase £18.73 by 17%
£18.73 x 1.17 1 = original 0.17 = 17%
Increase by 8%
£18.73 x 1.08
Decrease £18.73 by 17%
£18.73 x 0.83 0.83 = 1 - 0.17
Real Life Percentages
I save £500 in an account which pay intrest at 3% p.a. (per anum = every year)
After 1 year I have £500 x 1.03
After 2 years I have £500 x 1.03 x 1.03
After 10 years I have £500 x 1.0310
Proportion
If it costs £23 to paint a wall with the area of 13.52 what would it cost to paint an area of 22.9 m2?
£23 ÷ 13.5 = Cost of 1 square
£23 ÷ 13.5 x 22.9 = Cost of 22.9 m2?
It takes 5 people 8 days to paint a wall. How long would it take 4 people?
One person would take 40 days (5 x 8)
4 people would take 10 people (40 ÷ 4)
Collecting Like Terms
2a + 3b - a + 7b = a + 10b
5cd - 8ad + 2cd +15ad = 7cd +7ad
Expand
5 (3x - 2y) = 15x - 10y
-3 (4p - 7q) = -12p + 21q
x (x + y) = x2 + xy
3a (2a + 7b) 6a2 +21ab
5 (2a + 3b) - 3 (2a - 5b) = 10a + 15b - 6a + 15b
= 4a + 30b
x2 x x3 = xxxxxxxxx
= x
Nth Term
Nth term is n2 + 5
Write down the first 4 terms
6, 9, 14, 21
Working out the nth term
3, 7, 11, 15, 19
Each time we are adding 4 so there is 4n.
But it can't be just 4n because if we do 4n x 1 then it makes 4 but we want 3.The same with 4n x 2; we want 7 but 4 x 2 = 8 so the formula is:
4n - 1
Probability
The probability of something can on be from 0 -1.
So if something is impossible it would be 0 and if it was certain it would be 1.
The probability of a coin landing on heads is 1/2 or 0.5 as it is equally likely that it will land on heads or tails.
How likely it is to pick an ace from a pack of cards is 4/52, cancelling down to 1/13.
Perimeter
Perimeter is the distance around a two-dimensional shape.
Example 1: the perimeter of this rectangle is 7+3+7+3 = 20
The perimeter of a circle is called the circumference:
Related discussions on The Student Room
- Alevel combination (urgently needs help) »
- A level choices for imperial? »
- I have a lot OF A-level and GCSE Maths and Further Maths resources. Who's Interested? »
- A Level FM in one year or two »
- Any good revision resources/ websites for GCSE? »
- a level maths »
- Acturial science »
- Economics degree »
- A level further maths worth it »
- Maths vs Maths and Physics »
Comments
Report
Report