Circle Theorem

1. The angle at the centre is twice the angle at the circumference

2. The angle in a semicircle is a right angle

3. Angles in the same segment are equal

4. Opposite angles in a cyclic quadrilateral sum to 180°

5. The angle between the chord and the tangent is equal to the angle in the alternate segment

1. The angle at the centre is twice the angle at the circumference:

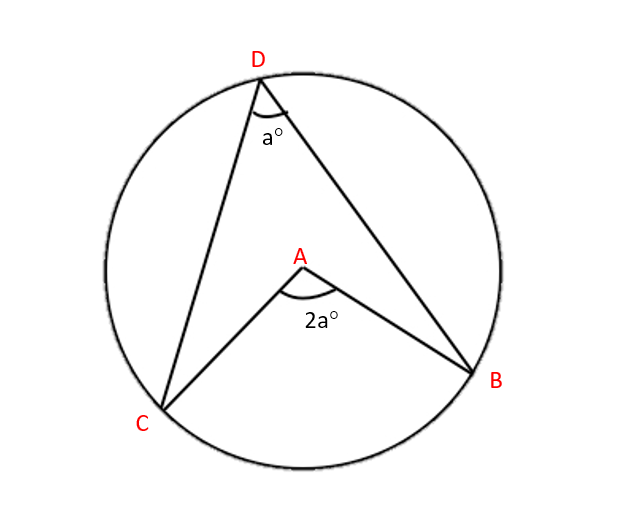
How do we show this? Start by drawing lines to connect A and D, and B and C. This forms three small triangles (∆ACD, ∆ABC, ∆ABD) and one big one (∆DCB). Since the lines AB, AC and AD are all radii of the circle, this means that the triangles ∆ACD, ∆ABD and ∆ABC are isosceles.

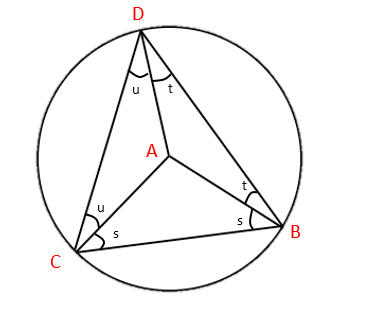
So we can see from ∆ABC that the angle at A is 180-2s (180° in a triangle).

And we have in the larger triangle ∆DCB that:

(u+s)+(u+t)+(t+s) = 180° (180° in a triangle).

which gives us:

2u+2t+2s = 180°

2u+2t = 180°-2s

= A

2. The angle in a semicircle is a right angle:

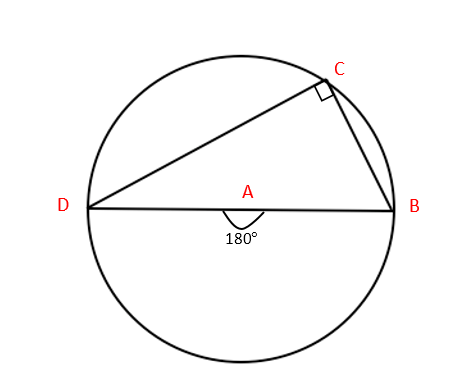
Firstly, we can see that this is an application of the theorem above, with angle at the centre = 180°. If we wanted to show this without using Theorem 1, start by drawing a line from A to C. Note that this is a radius of the circle. This makes three triangles: ∆ABC, ∆ACD and a large one, ∆BCD. We also have that ∆ABC and ∆ACD are isosceles.

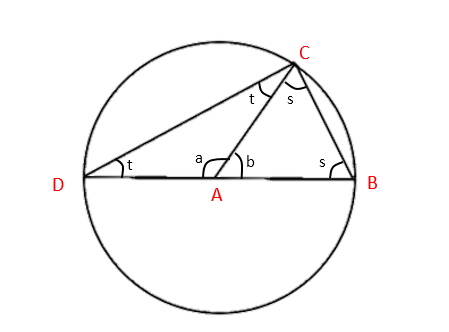
Firstly…