unit 4 section 1 simple harmonic motion and oscillators

SHM: an oscillation in which the acceleration is directly proportional  to its displacement from its equilibrium position, and is directed towards the equilibrium.

Displacement: x, varies as a cosine or a sine wave with a maximum value of A the amplitude.

Velocity: v, is the gradient of teh displacement-time graph. has a maximum value of (2pief)A, f is frequency of the oscillation.

Acceleration: a, is the gradient of the velocity-time graph. it has a maximum value of (2pief)2A.

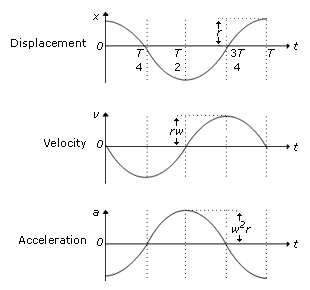
Phase difference: a measure of how much one wave lags behind another wave. it can be measured in degrees, radions or fractions of a cycle.

F=1/T

T=1/F

Frequency: number of complete revolutions or cycles that rotating or oscillating object makes per second.

Period: the time taken for a rotating or oscillating object to complete one revolution or cycle.

- as the object moves towards the equilibrium position, restoring force does work on the object and transfers EP to EK.

- when the object moves away from the equilibrium, all the EK is transferred back to EP again.

- at the equilibrium, the objects EP is zero and its EK is maximum - therefore its velocity is maximum.

- at maximum displacement on both sides of the equilibrium, the objects EP is maximum, and its EK is zero - so its velocity is zero.

Phase difference: a measure of how much one wave lags behind another wave. it can be measured in degrees, radions or fractions of a cycle.

F=1/T

T=1/F

Frequency: number of complete revolutions or cycles that rotating or oscillating object makes per second.

Period: the time taken for a rotating or oscillating object to complete one revolution or cycle.

SHO: a system that oscillates with SHM, like a simple pendulum

size and direction of the restoring force is shown with the equation:

- mass on a sping: F=-Kx

to

T=2pie x squareroot(m/K)

-simple pendulum:

- T=2pie x squareroot(l/g)